在JavaScript中如果在控制台中输入0.1+0.2会出现什么结果?正常来说结果是等于0.3的,令人惊讶的是,输出的结果却是:0.30000000000000004,究竟是什么原因使得JavaScript中0.1 + 0.2 !== 0.3,这就需要从JavaScript存储Number类型开始说起。
根据ECMAScript标准,数字只有一种类型,它是’双精度64位二进制格式IEEE 754值’。这个术语可能看起来有点有点复杂,请各位看官勿急着关闭,我们后面慢慢分析这个术语的意思。
科学记数法
在JavaScript中,数字都是以科学记数法,科学记数法的一般形式为
1 | significant * base^exponent |
这个表达式很容易理解,因为我们在初中数学中已经接触过科学记数法了。下面举一个栗子:
1 | 2 = 2 * 10^0 |
由于计算机是根据二进制来存储的,那么现在来看一下二进制下的科学记数法:
1 | 10 = 10 \* 2^0 = 1.0 \* 2^1 |
从上面的栗子可以看出,如果我们移动小数点的位置,可以通过改变指数的大小来保持数值的不变。也就是说,一个数字可以有多种科学记数法来表示。
如果我们定义科学记数法中前面的significant即有效位数的小数点前只有一位非零的数字,那么一个数字就只有一种这样的科学记数法表达式,我们称这种科学记数法表达式为标准化形式。
术语解析(浮点):因为在科学记数法中,小数点可以左右移动(它可以放在相对于数字有效数字的任何位置)而可以使整体数值保持不变,可以形象化地认为小数点在“浮动”,所以在编程语言中经常遇到的浮点数一般是指具有小数点的数。
IEEE 754标准
上面提到JavaScript数字只有一种类型,它是’双精度64位二进制格式IEEE 754值’,其中的IEEE 754是指一个标准,在这个标准里面定义了许多与浮点运算相关的内容,比如浮点的存储方式、舍入方式等等。也就是说,如果采用不同的标准,浮点的存储方式等都会不一样。
浮点的存储方式
标准定义了两种浮点最常用的格式:单精度和双精度,它们主要是指浮点在计算机中存储占用的位数(bit),一般来说,单精度主要指32位,双精度指64位。
所以现在我们可以知道“双精度64位二进制格式IEEE 754值”代表的是什么意思了:JavaScript的数字是根据IEEE 754标准,利用64位,以二进制的形式来存储的。
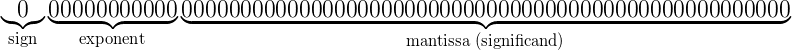
其结构为:
第一位:存储符号(正0负1),占 1 bit
第二位:存储指数(即科学记数法中的指数)占 11 bit
第三位:存储尾数(即科学记数法中的有效位数)占 52bit
下面来举一个栗子,比如数字 1:
- 首先将其化成二进制 1
- 然后化成标准化的科学记数法形式:
1 * 2^0 - 得到符号为
正,指数为0,尾数为1 - 利用上述的结构填入,得到:
0 00000000000 000000000000000000000000000000000000000000000000001
我们对比一下真实的存储:
0 01111111111 000000000000000000000000000000000000000000000000000
喂(#`O′),完全不对呀….
这个时候我们需要引入下面两个的概念来解释二者不同的原因:
小数点前 1 硬件前置
我们先回到数字1的标准化的科学记数法形式:1 * 2^0
前面讲过,小数点前面(此处为1)前不能为0,在二进制下,只有0和1,所以小数点前总是1(0的情况除外),因此如果小数点前面的一位数是1的话,那么就不需要进行存储,它会在计算的时候通过硬件前置,这样做的好处就是可以空出1位来存储内容。
因此,数字1的实际上存储的标准化的科学记数法形式是:.0 * 2^0,(小数点前的1通过硬件前置补回)
我们对比一下存储尾数的部分,也就是最长的那个部分,可以看到他们之间相差了最后的一个1。可见相差的那一个1就是省略的那一个1
解决了尾数结构的差异之后,再来解决一下指数部分的差异,即中间部分。稍微比较一下两者,发现二者不是相差一个1那么简单啊(虽然真的只是相差1(⊙﹏⊙))
其实在标准下,JavaScript是通过偏移二进制来存储指数部分的。
偏移二进制
在讲解偏移二进制之前先举一个栗子:
假设我们只有4位可以用来存储数字,那么4位可以存储的数字为:2^4 = 16个数字
也就是说我们能够在4位中存储[0, 15]的数字
那么如果我想存储负数呢?比如[-1, 14]
这个时候就要引入偏移的概念了,因为计算机存储的二进制永远只能是[0, 15]的数据,即[0000, 1111],那么我们定义一个映射:f(x) = x - k,其中k就代表位偏移量。假设 k = 1,便可以建立下面的映射:
| 计算机实际存储内容(用十进制表示) | 存储内容 |
|---|---|
| 0 | -1 |
| 1 | 0 |
| … | … |
| 15 | 14 |
可以简单地这样理解偏移二进制:偏移二进制是通过引入偏移量k来改变存储数值范围的。
偏移量k可以自由定义,在标准中,偏移量可以通过下面的公式计算得出:
K = 2^(n - 1) - 1
所以在11位(指数存储位数)中,偏移量K = 2^(11 - 1) - 1 = 1023
因为我们存储的指数0需要通过公式f(x) = x - k => x = f(x) + k来换算,即得到x = 1023,用二进制表示为01111111111
0.1 + 0.2 !== 0.3
这样我们知道了JavaScript中数字的存储规律,现在我们利用它来解释一下为什么0.1 + 0.2 !== 0.3
首先我们要将二者变成计算机中存储的格式,嗯?!,小数怎么化成二进制?
将小数转换为二进制方法
从相关小鼠开始并将其乘以2,注意结果整数和小数部分。继续乘以2,直到得到的结果小数部分等于零。然后从每次乘法的结果中写出整数部分。
以0.2为栗子,
1 | 0.2 * 2 = 0 + 0.4 |
所以最终得到的结果是0.(0011) 的无限循环,化简之后为1.(1001) * 2^-3
得到二进制的科学记数法之后,可以发现其具有无限循环结构,也就是说,尾数的52位无法容纳无限位数,必然会采取舍去操作。因此实际上存储的0.2数值上会与真实值不一样,而这个差异以及取舍规则导致了上述结果的根本原因。
Reference
Here is what you need to know about JavaScript’s Number type


